Découvrez Comment Déterminer Le Point De Rencontre Des Hauteurs Dans Un Triangle, Un Concept Clé En Géométrie. Maîtrisez Cette Notion Essentielle Avec Notre Guide Complet.

**calculer Le Point De Rencontre Des Hauteurs**

• Les Concepts Fondamentaux Des Hauteurs En Géométrie
• Comment Établir Les Hauteurs D’un Triangle
• La Méthode De Construction Du Point De Rencontre
• Applications Pratiques Du Point De Rencontre Des Hauteurs
• Études De Cas : Exemples Géométriques Concrets
• Erreurs Courantes À Éviter Lors Des Calculs

Les Concepts Fondamentaux Des Hauteurs En Géométrie

Dans le monde fascinant de la géométrie, la notion de hauteur revêt une importance capitale. En effet, chaque triangle possède trois hauteurs, qui sont des segments perpendiculaires reliant un sommet au côté opposé. Ces longueurs sont essentielles, car elles permettent de déterminer des propriétés cruciales du triangle, mais également de faciliter des calculs plus complexes. En geometry, la hauteur est bien plus qu’une simple mesure : elle est le point de départ d’un vaste ensemble de relations et de théorèmes qui mènent à la compréhension de structures géométriques plus avancées.

Lorsqu’on aborde la notion de hauteur, il est important de garder à l’esprit que la précision est l’un des éléments clés. Ainsi, les méthodes de construction des hauteurs doivent être rigoureusement appliquées pour éviter toute erreur. Par exemple, lors de la réalisation d’un triangle, si une hauteur n’est pas dessinée directement, on peut facilement se perdre dans des calculs minutieux. Les hauteurs sont souvent utilisées dans diverses applications pratiques, qu’il s’agisse de théorèmes géométriques fondamentaux ou de problèmes plus appliqués en architecture et en ingénierie.

L’illustration et la visualisation des hauteurs aident à mieux comprendre leur rôle. Imaginons un triangle équilatéral, où toutes les hauteurs se rencontrent en un point unique, le centre de gravité. Ce point, souvent considéré comme un “point magique”, permet de vérifier l’harmonie des dimensions et de l’équilibre du triangle. C’est ici que la beauté de la géométrie se manifeste, comme une formule complexe à l’intérieur d’un tableau. En somme, les hauteurs et leur intersection constituent un axe fondamental pour explorer le vaste univers de la géométrie.

Type de Triangle	Nombre de Hauteurs	Description
Équilatéral	3	Toutes les hauteurs se rencontrent au centre de gravité.
Isocèle	3	Deux hauteurs sont égales et la troisième est différente.
Scalène	3	Toutes les hauteurs sont différentes.

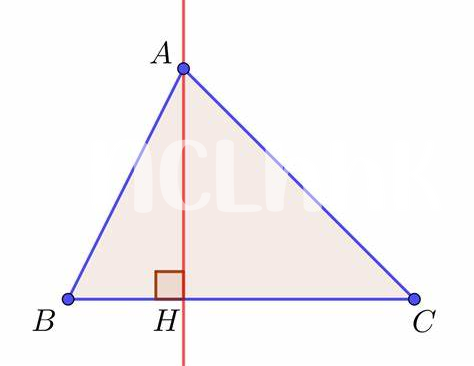
Comment Établir Les Hauteurs D’un Triangle

Dans un triangle, établir les hauteurs est une étape cruciale qui permet d’identifier le point de rencontre des hauteurs dans un triangle. Pour ce faire, il est essentiel de comprendre que la hauteur d’un triangle est la distance perpendiculaire d’un sommet à la droite opposée, souvent appelée base. Chaque triangle possède trois sommets et, par conséquent, trois hauteurs distinctes. Pour calculer ces hauteurs, il faut d’abord déterminer la longueur de la base et l’aire du triangle.

Un moyen efficace pour établir une hauteur est d’utiliser la formule de l’aire, qui est donnée par : Aire = (base × hauteur) / 2. En réarrangeant cette formule, nous pouvons exprimer la hauteur : hauteur = (2 × Aire) / base. En obtenant l’aire du triangle, que l’on peut calculer avec différentes méthodes, y compris la formule de Héron, il devient plus facile de déduire la hauteur.

Par exemple, prenons un triangle de base 10 unités et d’aire 20 unités carrées. En appliquant notre formule, on obtient : hauteur = (2 × 20) / 10, soit une hauteur de 4 unités. Il est important de noter que les hauteurs peuvent parfois sembler déroutantes, surtout si elles ne se trouvent pas à l’intérieur du triangle, en particulier dans le cas des triangles obtus.

Une fois les hauteurs établies, il ne reste plus qu’à tracer ces segments pour localiser le point d’intersection. Ce processus peut sembler technique, mais en s’y prenant méthodiquement, il devient plus accessible, et vous serez en mesure de naviguer sans heurt dans l’univers fascinant de la géométrie.

La Méthode De Construction Du Point De Rencontre

Pour établir le point de rencontre des hauteurs dans un triangle, il est essentiel de comprendre les hauteurs elles-mêmes. Chaque hauteur d’un triangle est la perpendicularité tracée depuis un sommet jusqu’au côté opposé. En utilisant un compas et une règle, nous pouvons procéder à la construction de ces hauteurs. Commencez par tracer le triangle sur votre papier, en notant soigneusement les sommets. Cela vous permettra de visualiser où chaque hauteur doit être dessinée.

Une méthode efficace consiste à prendre un sommet du triangle et à tracer une ligne perpendiculaire au côté opposé. Pour ce faire, placez votre équerre de manière à obtenir un angle de 90 degrés avec le côté. Ensuite, prolongez cette ligne jusqu’à ce qu’elle croise le côté. Répétez ce processus pour les deux autres sommets, en glissant votre règle le long des côtés respectifs pour garantir une précision. Une fois toutes les hauteurs tracées, leurs intersections deviendront le point de rencontre des hauteurs.

Il est important de vérifier que chaque hauteur est bien perpendiculaire, car même un petit écart peut affecter le résultat final. En utilisant ce schéma, notez où toutes les lignes se rejoignent. Ce point, au sein du triangle, est réputé pour ses propriétés uniques, notamment en ce qui concerne les centres de gravité et les équilibres au sein des figures géométriques.

Enfin, n’oubliez pas qu’une erreur courante est de ne pas créer des lignes suffisamment longues qui peuvent rendre le point de rencontre difficile à identifier. Soyez précis dans votre construction et n’hésitez pas à utiliser des outils tels que des rapporteurs pour assurer la qualité de votre travail. En suivant ces étapes, vous pourrez facilement réussir à établir le tant convoité point de rencontre.

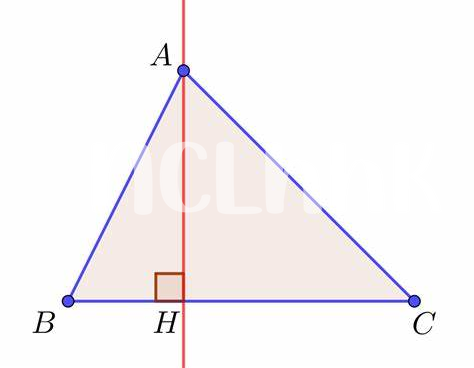
Applications Pratiques Du Point De Rencontre Des Hauteurs

Le point de rencontre des hauteurs dans un triangle joue un rôle crucial dans diverses applications pratiques, notamment dans le domaine de l’architecture et de l’ingénierie. Par exemple, les architectes utilisent ce concept pour déterminer les points critiques qui influencent la stabilité des structures. En construisant des murs et des toits, connaître les intersections des hauteurs permet d’assurer une meilleure répartition des forces, ce qui est essentiel pour éviter tout effondrement. Ce calcul devient encore plus significatif lors de la conception de structures complexes, où chaque élément doit se soutenir mutuellement, semblable à la manière dont les “Happy Pills” aident à équilibrer le bien-être mental dans une approche holistique.

Dans le domaine de la navigation et de la cartographie, le point de rencontre des hauteurs est également vital. Les géomètres et les cartographes s’en servent pour établir des repères géographiques précis, assurant ainsi un positionnement fiable des lieux. Par analogie, c’est un peu comme le processus “Count and Pour” en pharmacie, où chaque mouvement est mesuré pour garantir un dosage correct. Une erreur dans le calcul peut mener à des imprécisions significatives, affectant à la fois l’architecture et la navigation, tout comme des prescriptions mal remplies peuvent nuire à la santé d’un patient.

Enfin, dans le cadre de la recherche académique et de l’enseignement, l’étude du point de rencontre des hauteurs facilite la compréhension des concepts géométriques avancés. Les enseignants l’utilisent comme un outil pédagogique pour expliquer la relation entre les différentes lignes dans un triangle, rendant l’apprentissage plus engageant et accessible. En intégrant des méthodes variées, comme des simulations en ligne, ils peuvent transformer l’apprentissage en une expérience interactive, semblable à la manière dont un “Pharm Party” apporte une dynamique sociale à l’échange d’informations, en favorisant l’interaction et la découverte entre pairs.

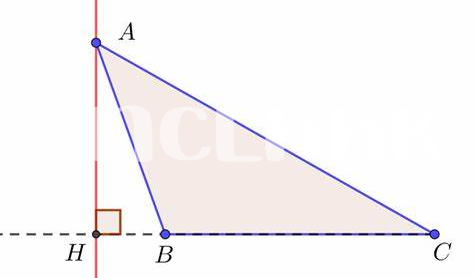
Études De Cas : Exemples Géométriques Concrets

L’étude des triangles offre un terrain fascinant pour explorer le point de rencontre des hauteurs, et plusieurs exemples concrets illustrent parfaitement ce concept. Prenons le triangle équilatéral, où les trois hauteurs se rencontrent en un seul point central. Ce point de rencontre est également le centre de gravité du triangle, ce qui montre l’harmonie géométrique à l’œuvre. En traçant chaque hauteur, nous pouvons observer que, peu importe comment nous orientons le triangle, le point de rencontre des hauteurs dans un triangle reste invariant. Cette caractéristique est unique et permet d’appliquer des principes de symétrie dans des problèmes géométriques complexes.

Une autre illustration frappante peut être observée dans les triangles isocèles. Ici, deux hauteurs se rencontrent à un point qui n’est pas nécessairement le centre de gravité, mais qui dépend de la base du triangle. Imaginons un triangle dont les côtés mesurent respectivement 6, 6, et 4 cm. En traçant les hauteurs depuis les sommets des deux côtés égaux, nous remarquons que le point de rencontre des hauteurs se situe encore sur la ligne médiane qui divise la base en deux segments égaux. Cette propriété renforce la notion de répartition et d’équilibre dans la structure du triangle.

D’autres formes de triangles, comme les triangles scalènes, ajoutent un niveau de défi supplémentaire. Dans un triangle scalène, les hauteurs mènent à un point de rencontre également, mais celui-ci est souvent éloigné des centres de symétrie. Le calcul ici implique des mesures précises et peut nécessiter des formules plus complexes. La détermination du point de rencontre des hauteurs dans ces triangles démontre non seulement la diversité des triangles mais également l’adaptabilité des méthodes géométriques.

Enfin, pour donner un aperçu pratique, une simple table peut être un outil utile pour compter le nombre de segments et évaluer les longueurs des hauteurs, permettant ainsi une visualisation claire des relations entre les points, les côtés et les angles. Une telle approche systématique facilite l’identification des erreurs courantes, prévenant ainsi des résultats erronés lors des calculs.

Type de triangle	Caractéristique	Exemple de calcul
Équilatéral	Point de rencontre au centre	Hauteur = (√3 / 2) * côté
Isocèle	Point de rencontre sur la médiane	Base divise en segments égaux
Scalène	Point de rencontre décalé	Utilisation de formules complexes

Erreurs Courantes À Éviter Lors Des Calculs

Lors de l’établissement du point de rencontre des hauteurs d’un triangle, il est facile de commettre des erreurs qui peuvent fausser les résultats. Un des problèmes courants est de confondre les altitudes avec d’autres éléments du triangle, comme les médianes ou les bissectrices. Cette méprise peut survenir lorsque l’on calque une méthode sans bien comprendre les spécificités de chaque segment. Pour éviter cela, il est essentiel de prendre du temps pour bien visualiser le triangle et comprendre la place et la fonction de chaque hauteur.

Une autre erreur fréquente consiste à ne pas vérifier soigneusement les mesures des côtés du triangle. Par exemple, une longueur mal notée peut provoquer des dérives significatives dans les calculs. L’addition ou la soustraction mal effectuée peut aussi se révéler catastrophique. S’assurer de la précision des mesures, tout comme dans le domaine pharmaceutique où un ‘Hard Copy’ est vital, doit être une priorité. Chaque valeur doit être revue avec attention pour garantir un résultat final fiable.

De plus, ignorer les propriétés géométriques des triangles peut également engendrer des problèmes. Certains utilisateurs peuvent appliquer des formules sans prendre en compte les règles de base relatives à la somme des angles ou même à la nature du triangle lui-même. Pour illustrer ce point, on peut penser à un ‘Pharm Party’ où les participants échangent des informations erronées sur les prescriptions, entraînant des confusions conséquentes.

Enfin, négliger la vérification des solutions est une autre source d’erreurs. Après avoir effectué des calculs, il est crucial de revenir sur les résultats obtenus pour s’assurer qu’ils sont cohérents entre eux. Comme pour un traitement médical, où le bénéfice doit être évalué, ici aussi, la précision des calculs doit être scrutée. Ne pas le faire peut aboutir à des conclusions erronées qui nuiraient à l’analyse géométrique.